【ベストコレクション】 reflection over x and y axis equation 273965-Reflection over x or y axis in equation

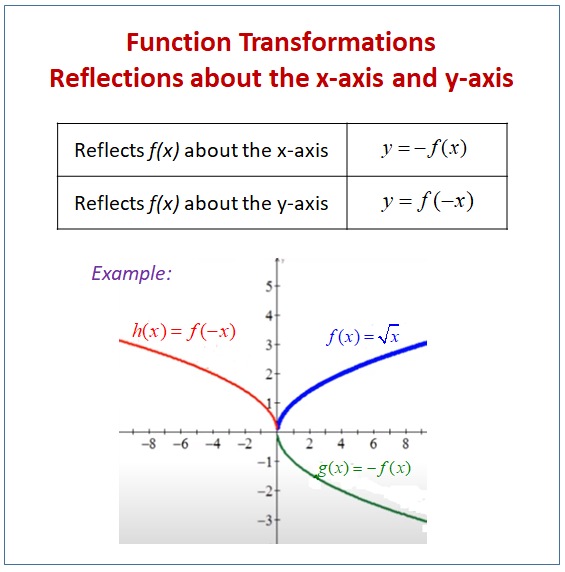
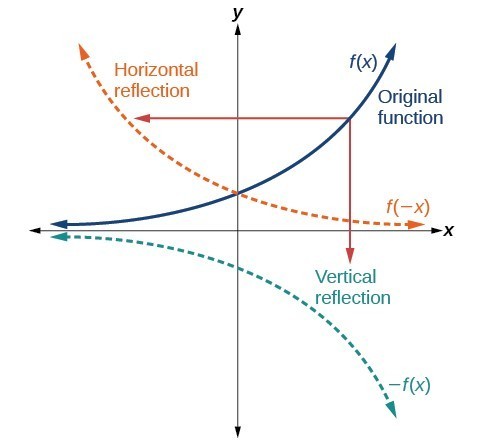
The equation of the line of symmetry To describe a reflection on a grid, the equation of the mirror line is needed Example Reflect the shape in the line \(x = 1\) The line \(x = 1\) is aF ( x) \displaystyle f\left (x\right) f (x), a new function g ( x) = f ( − x) \displaystyle g\left (x\right)=f\left (x\right) g(x) = f (−x) is a horizontal reflection of the function f ( x) \displaystyle f\left (x\right) f (x), sometimes called a reflection about the y axisThe rule for a reflection over the x axis is (x,y)→(x,−y) What is true reflection?

What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic

Reflection over x or y axis in equation

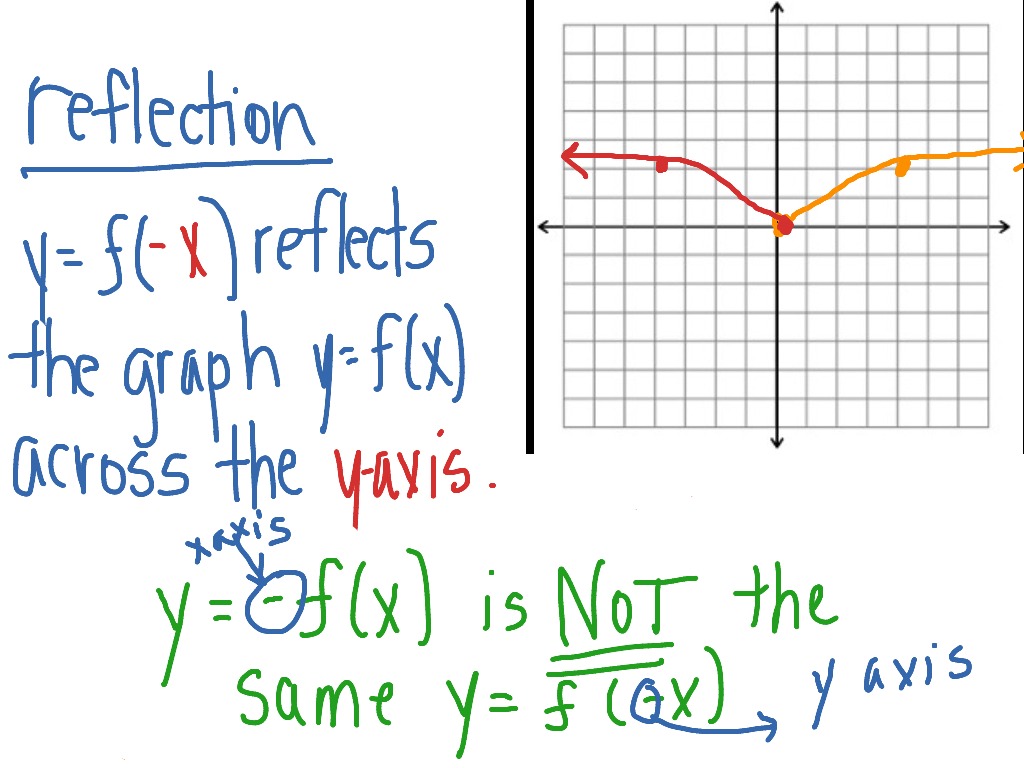
Reflection over x or y axis in equation-Reflection across the yaxis y = f ( − x ) y = f (x) y=f (−x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxis, and vice versaStack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

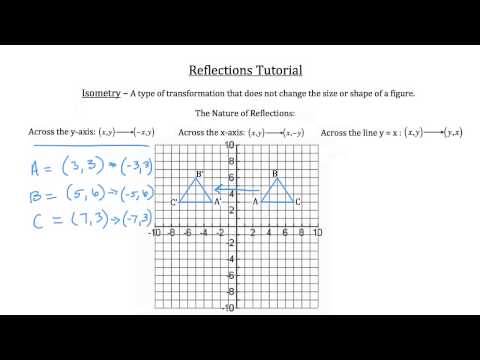
Reflection Notes Videos Qa And Tests Grade 9 Optional Mathematics Transformation Kullabs

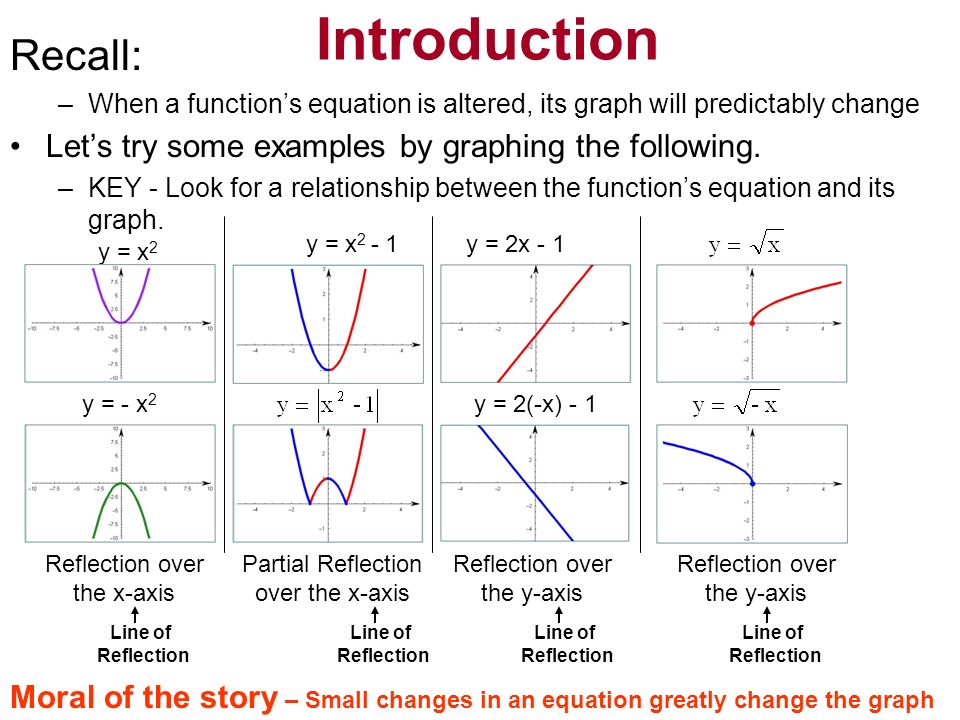
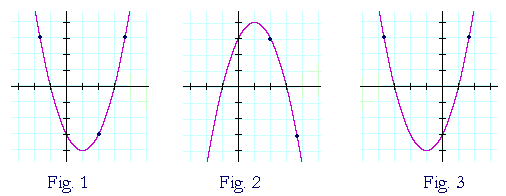
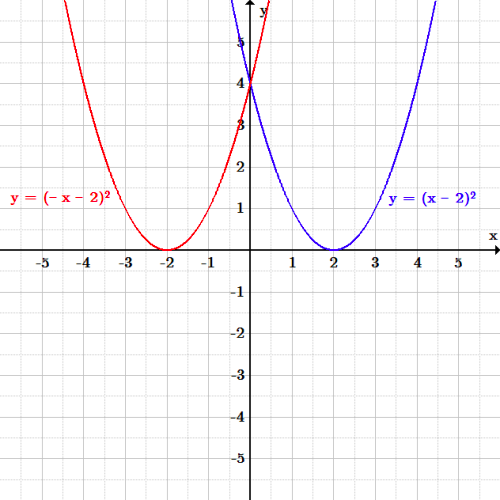
Apply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvalues This is a different form of the transformation Let's work with point A first Since it will be a horizontal reflection, where the reflection is over x=3, we first need to determine the distance of the xvalue of point A to the line of reflectionWrite the equation for the final transformed graph of f after the indicated transformations are applied to its graph f(x) = 4\sqrt{x}, reflect in the yaxis and shift upwards 5 unitsFig 3 is the reflection of Fig 1 about the yaxis Every point that was to the right of the origin gets reflected to the left And every point that was on the left gets reflected to the right In other words—every x becomes −x Only the yintercept is invariant The equation of the reflection of f(x) about the yaxis is y = f(−x)

Rewrite the equation by factoring out a 1 from the exponent to read From the equation, you can see that the horizontal shift will be to the left 10 units and there will be a reflection over the yaxisTherefore, reflect the graph of over the yaxis and then shift (move) the reflected graph left 10 unitsReflection over the xaxis is a type of linear transformation that flips a shape or graph over the xaxis Every point above the xaxis is reflected to its corresponding position below the xaxis;Geometry reflection A reflection is a flip of an object over a line Let's look at two very common reflections a horizontal reflection and a vertical reflection

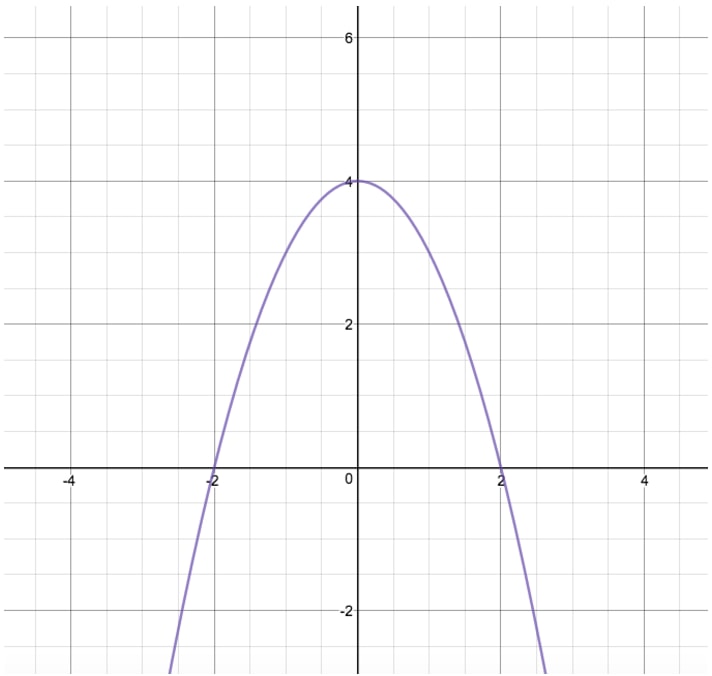
The reflection of such a parabola over the xaxis is simply written as y = (x^2) In other words, the function of f ( x ) becomes f ( x ) when reflected over the x axisReflection over x axis equation Since the reflection applied is going to be over the xaxis that means negating the yvalue For example if we begin by graphing the parent function latexfleftxright2xlatex we can then graph the two reflections We are not concerned about other transformations that take F x displaystyle fleft xright f x a new functionIdentifying coordinates of figures' reflections In this lesson students examine the impact on coordinates when a figure is reflected over the xaxis and yaxis They also learn to apply algebraic representations and analyze graphed images Students learn that a reflection is a mirror image of a figure over the line of reflection

Transforming Exponential Functions

Want Brainliest Get This Correct What Is The Equation Of This Function After It Is Reflected Over Brainly Com

Remember that when a point P (x, y) of the coordinate plane is reflected in the y axis , it becomes the point Q (x, y) and when reflected in x axis, it becomes P' (x, y) Therefore the quadratic p (x) = ax^2 bx c (a not zero) when reflected in y axis it becomes ;I start with e^x which is a curve that follows y=0 then starts to rise more abruptly at x=0 If f (x) Makes you reflect over the x axis Then e^x will do a neccesary reflection for reflecting it about y = 2 Then I add 2 to the end of f (x) = (e^x)2 = 2e^x Although on my homework they say the correct answer is 4 e^xReflection across the yaxis y = f ( − x) y = f (x) y = f ( − x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxis, and vice versa Basic Concepts

Reflecting Functions Or Graphs Examples Solutions Worksheets Videos Games Activities

How To Horizontally Transform A Function Dummies

An image created by a reflection will always be congruent to its preimageIt makes sense but at he same time it doesn't because when I pump the reflectedSo that would end up giving us why Subtract the X over equals negative X plus one And we're going to go ahead and plot this up until the X axis And so it's going to start up at positive one

Ch 3 4

How To Reflect A Graph Through The X Axis Studypug

In that light being originates from the second quadrant with the equation X plus y equals one We could go ahead and rearrange that and solve for why?This video explains to graph graph reflections across the xaxis and yaxis in the form a*f(b(xc))d This video looks at how the sign of a and b affect thThereof, how do you reflect a log over the y axis?

Unit 6 Topic 2 Other Line Reflections Williamsburg High School For Architecture And Design

Parabola Scalings And Translations Zona Land Education

Reflection across the yaxis y = f ( − x ) y = f (x) y=f (−x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxis, and vice versaIs the graph of y=x²Step 1 Know that we're reflecting across the xaxis Since we were asked to plot the – f (x) f(x) f (x) reflection, is it very important that you recognize this means we are being asked to plot the reflection over the xaxis When drawing reflections across the x x x and y y y axis, it is very easy to get confused by some of the notations

Reflection Notes Videos Qa And Tests Grade 9 Optional Mathematics Transformation Kullabs

Assignment 2 Transforming Parabolas

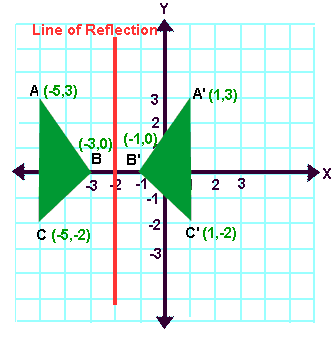
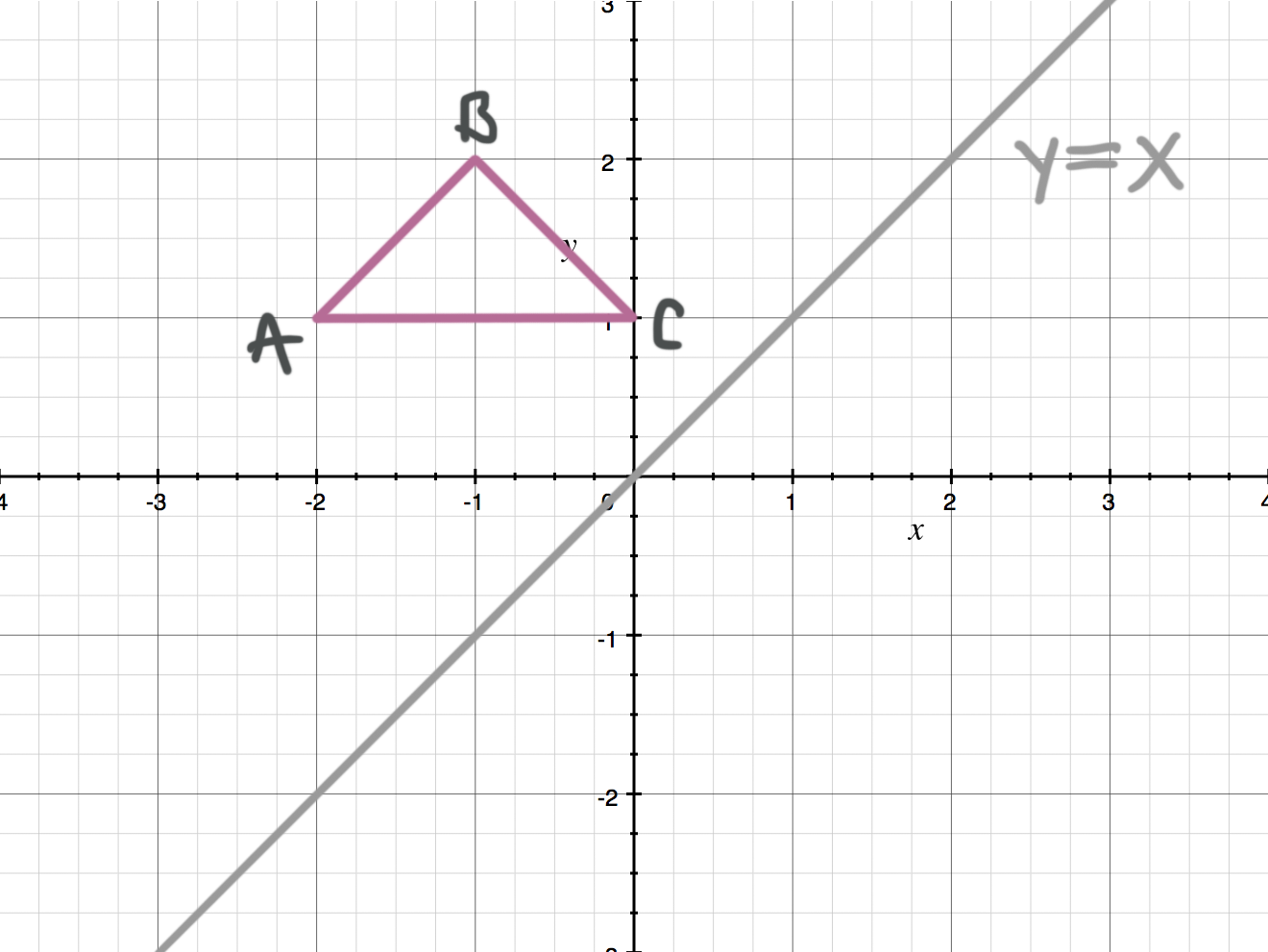
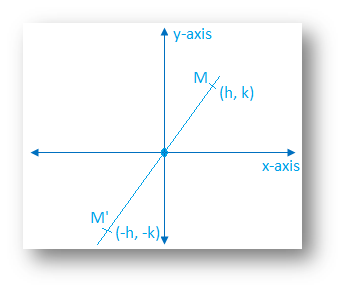
And also, the line x = 2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image Students can keep this idea in mind when they are working with lines of reflections which are neither the xaxis nor the yaxisWhen reflecting coordinate points of the preimage over the line, the following notation can be used to determine the coordinate points of the image r y=x =(y,x) For example For triangle ABC with coordinate points A(3,3), B(2,1), and C(6,2), apply a reflection over the line y=x By following the notation, we would swap the xvalue and the yvalueReflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (B, A ) $

Transformations Ib Math Stuff

Cartesian Coordinate System Wikipedia

Scaled by a factor of k If k<0, it's also reflected (or flipped) across the xaxis In this worked example, we find the equation of a parabola from its graph Transforming quadratic functions Intro to parabola transformationsFunctions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to design objects and imagesReflection A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a line of symmetry using a reflection matrix

Reflection Transformation Matrix

Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download

Odd Function A function f f is called an odd function if f(x)= −f(−x) f ( x) = − f ( − x) for all x x in the domain of f f In other words, a function is odd if performing a reflection about the y y axis and x x axis (doesn't matter which is performed first) does not change the graph of the function To help remember the definitionWhen you reflect a point across the yaxis, the ycoordinate remains the same, but the xcoordinate is transformed into its opposite When working with the graph of y = f (x), replace x with x Reflection in y = x When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change placesThe relection of the graph of f( x,y) = 0 in the xaxis is f(x, —y) = 0 So the image of the line y=2x in the xaxis is —y = 2x or y = —2x

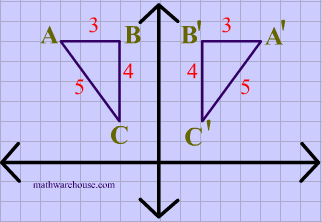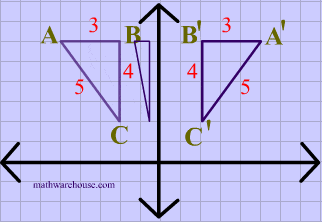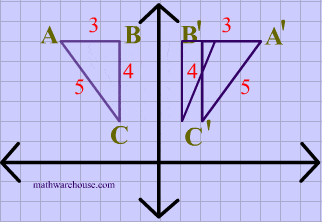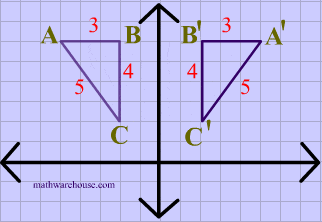
Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines

Question Video Writing The Equation For A Square Root Function Obtained By A Reflection In The 𝑦 Axis Nagwa

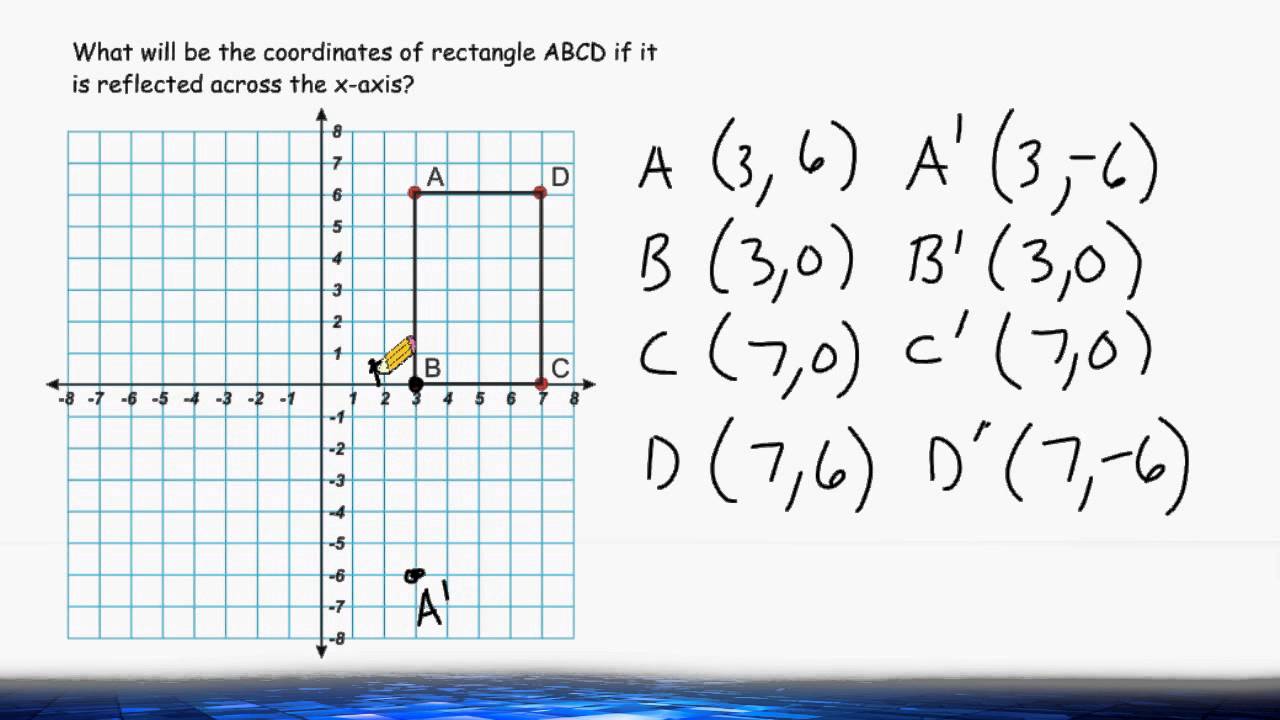
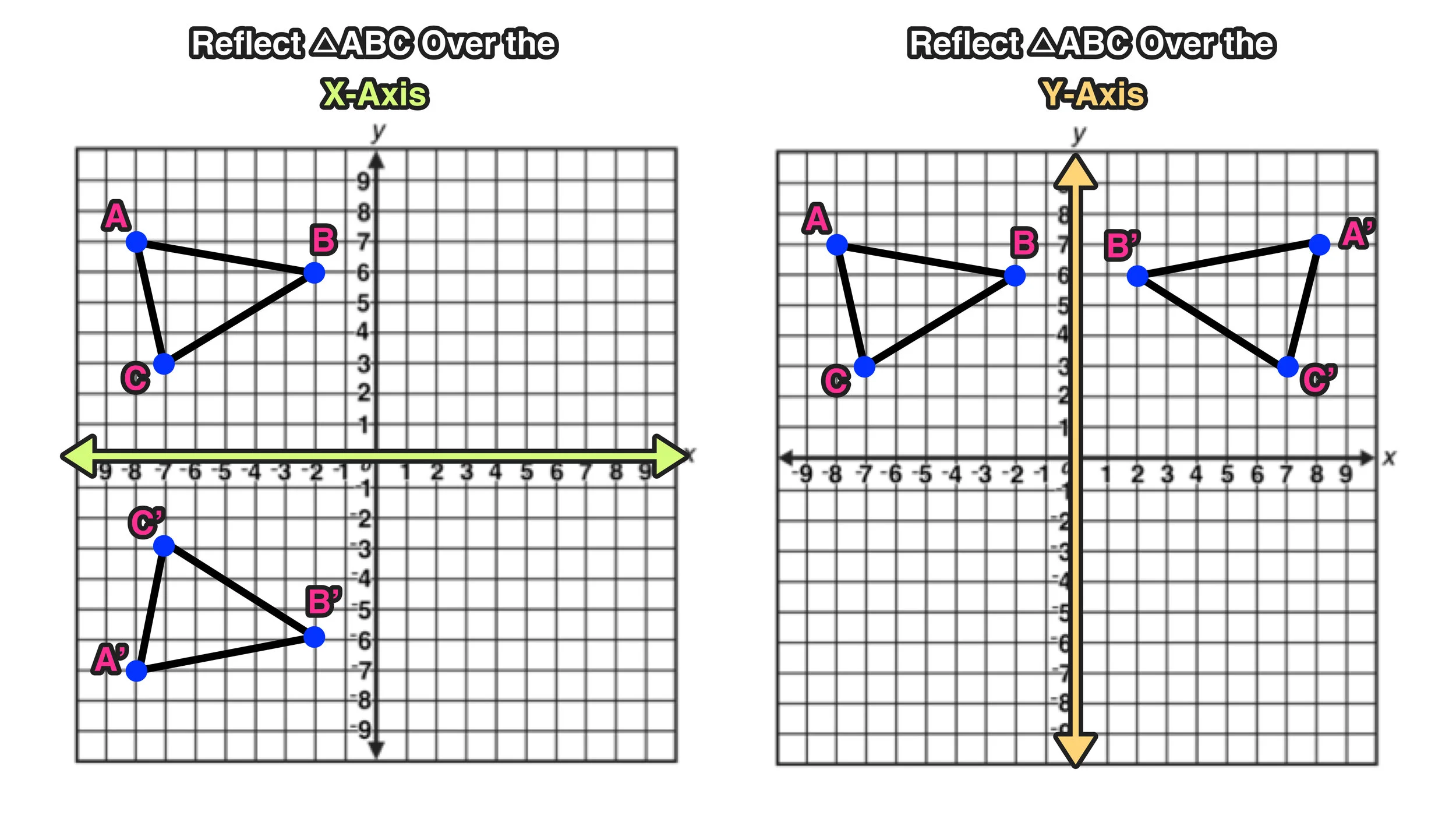
Every point below the xaxis is reflected to its corresponding position above the xaxis Contents Reflection over the xaxis for Sets of Coordinates (x, y),Example 3 Triangle PQR has the vertices P(2, 5), Q(6, 2) and R(2, 2) Find the vertices of triangle P'Q'R' after a reflection across the xaxis Then graph the triangle and its image Solution Step 1 Apply the rule to find the vertices of the imageGraphing Reflections In addition to shifting, compressing, and stretching a graph, we can also reflect it about the x axis or the y axis When we multiply the parent function f (x) = bx f ( x) = b x by –1, we get a reflection about the x axis When we multiply the input by –1, we get a reflection about the y axis

A Review Of Logarithms

Content Transformations Of The Parabola

This video shows reflection over the xaxis, yaxis, x = −3, y = 5, y = x, and y = − x Show Video Lesson Reflections using Matrices This lesson involves reflections in the coordinate plane We use coordinate rules as well as matrix multiplication to reflect a polygon (or polygon matrix) about the xaxis, yaxis, the line y = x or theOn this lesson, you will learn how to perform reflections over the xaxis and reflections over the yaxis (also known as across the xaxis and across the yaWe can reflect the graph of any function f about the xaxis by graphing y=f (x) and we can reflect it about the yaxis by graphing y=f (x) We can even reflect it about both axes by graphing y=f (x) See how this is applied to solve various problems Google Classroom Facebook Twitter Email

Content Transformations Of The Parabola

Solved The Graph Shown To The Right Involves A Reflection In Chegg Com

The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point, but leave the xvalue the same For example, when point P with coordinates (5,4) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,4)Reflections in Math Applet Interactive Reflections in Math Explorer Demonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y =The transformation from the first equation to the second one can be found by finding a a, h h, and k k for each equation y = a√x− hk y = a x h k Factor a 1 1 out of the absolute value to make the coefficient of x x equal to 1 1 y = √x y = x Find a a, h h, and k k for y = √x y = x a = 1 a = 1

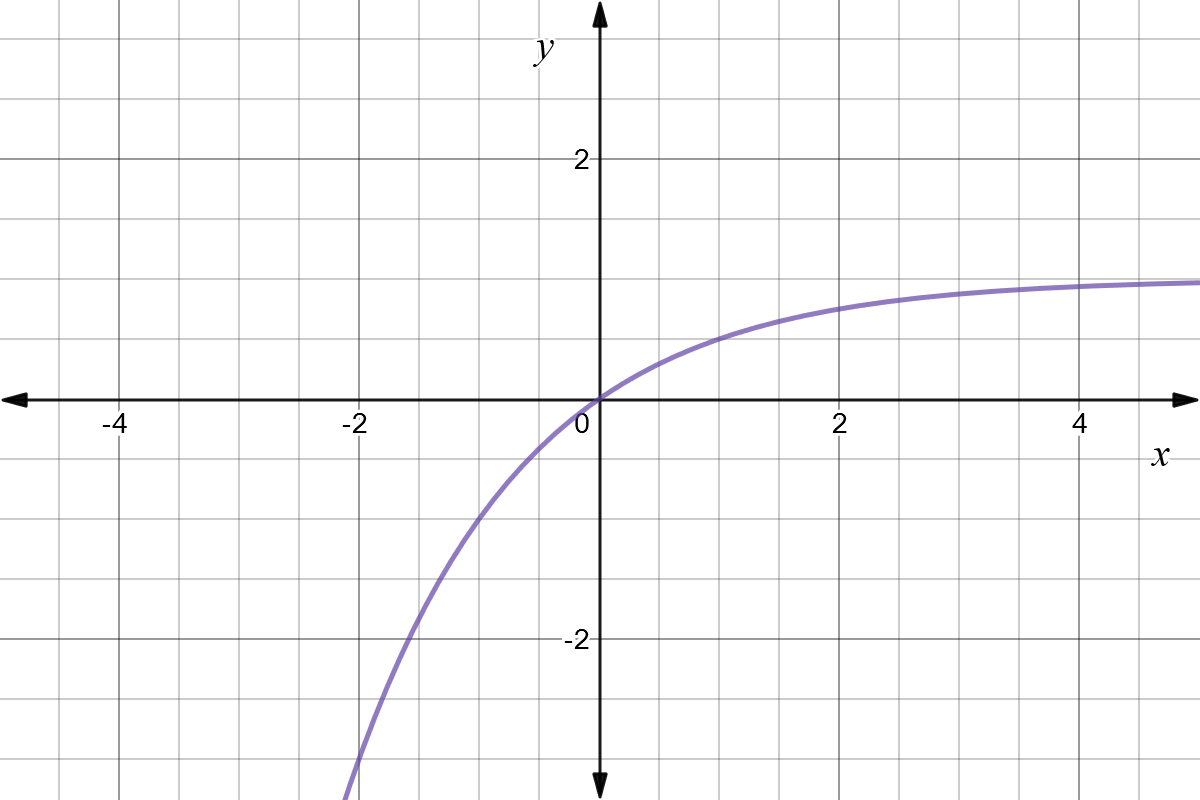
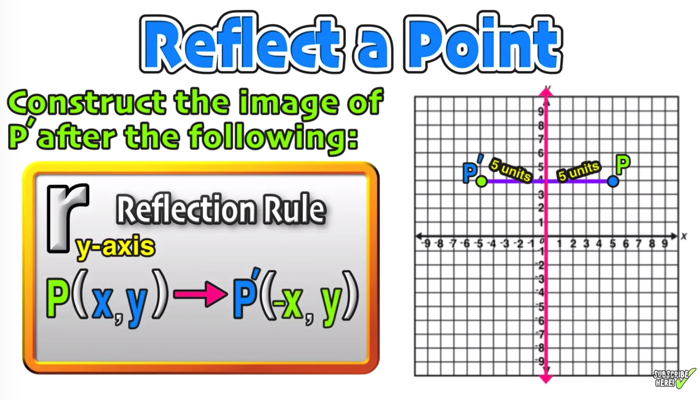
Reflect Function About Y Axis F X Expii

Assignment 2 Transforming Parabolas

Y axis) Reflection over line y=x or y=Reflection over line y=x or y=xx Reflection over y=x Point (x,y) reflects to point (y,x) Reflection over line y=xThe answer from question (1) is reflected in the line x = 4 What is the equation of the image?A math reflection flips a graph over the yaxis, and is of the form y = f (x) Other important transformations include vertical shifts, horizontal shifts and horizontal compression Let's talk about reflections Now recall how to reflect the graph y=f of x across the x axis

1

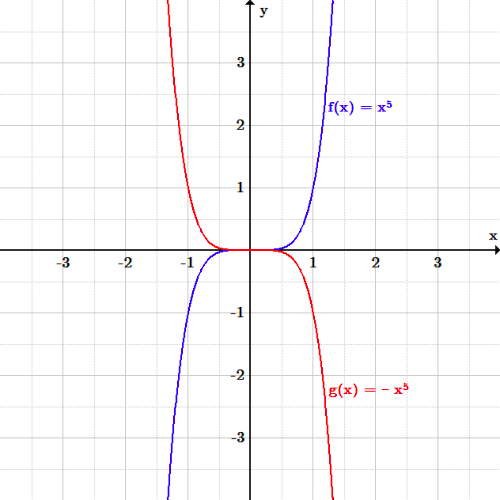
Transformations Boundless Algebra

Reflect Over XAxis Definition Reflection over the xaxis is the process of producing a coordinate point that is mirrored across the xaxis of the coordinate plane That is it has the same X coordinate and opposite y4 coordinateReflection of the square root function over the yaxis Square Root Function Reflection of the Square Root Function across the yaxis Now, I know the domain of a square root has to be equal to or greater than zero So that's when imaginary numbers are used Right?The graph of y=k⋅x²

Polar Graph Polar Equation Symmetry Reflection X Axis Symmetric About The X Axis Homework Help Videos Brightstorm

How To Reflect A Graph Through The X Axis Studypug

A reflection of a point over the x axis is shown The rule for a reflection over the x axis is ( x, y) → ( x, − y)The line y = 15x – 2 is reflected in the line y = 1 What is the equation of the image?

A Review Of Logarithms

Reflection Over The X And Y Axis The Complete Guide Mashup Math

Operations On Functions Reflections And Rotations Sparknotes

Assignment 2 Transforming Parabolas

1 5 Shifting Reflecting And Stretching Graphs

Pre Cal 40s Fall 06 Scribe Transformation

What Is The Equation Of This Function After It Is Reflected Over The X Axis Brainly Com

Reflections Of A Graph Topics In Precalculus

Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor

How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics

Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra

Transformations Reflection Across The X Axis Youtube

Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines

Operations On Functions Reflections And Rotations Sparknotes

What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic

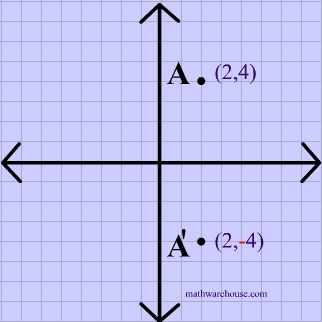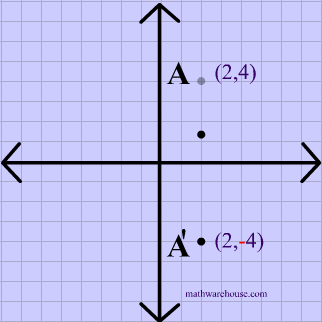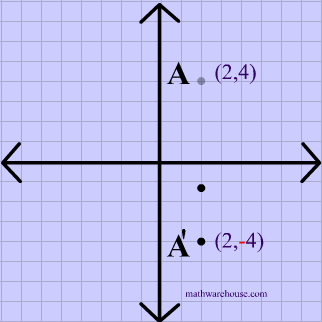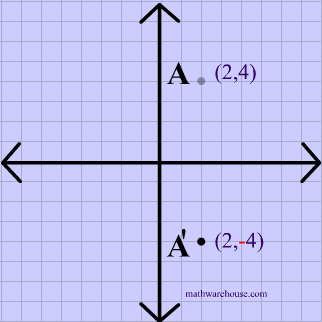
Reflection Across The Y Axis Math Functions Showme

How To Find The Equation Of The Graph Reflected About A Line Mathematics Stack Exchange

Reflection Transformation Matrix

Transformations Of Functions Mathbitsnotebook A1 Ccss Math

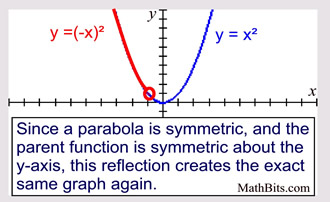
Parabola Parent Function Mathbitsnotebook A1 Ccss Math

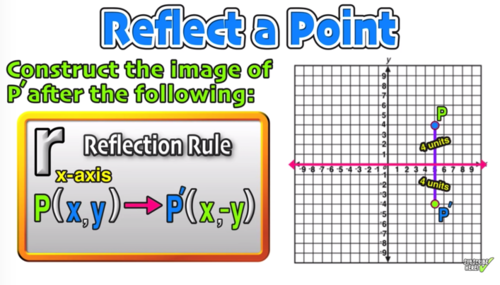
Reflection Over The X And Y Axis The Complete Guide Mashup Math

Learn About Reflection Over The Line Y X Caddell Prep Online

Reflection Across The X Axis Reflection Math Chart

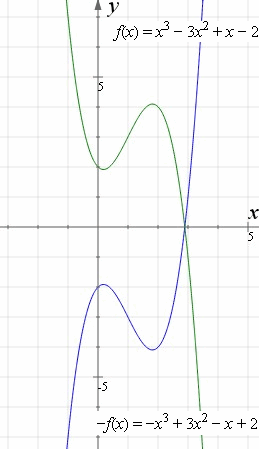
How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics

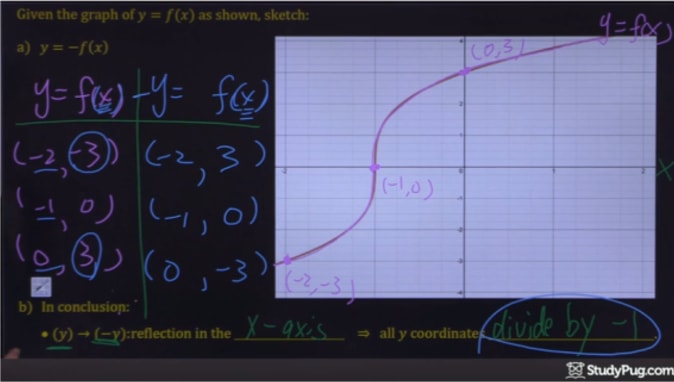
How To Reflect A Graph Through The X Axis Studypug

Reflection Rules How To W 25 Step By Step Examples

Function Transformations Reflections Across The X Axis And Y Axis Math Help From Arithmetic Through Calculus And Beyond

Reflect Function About Y Axis F X Expii

How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com

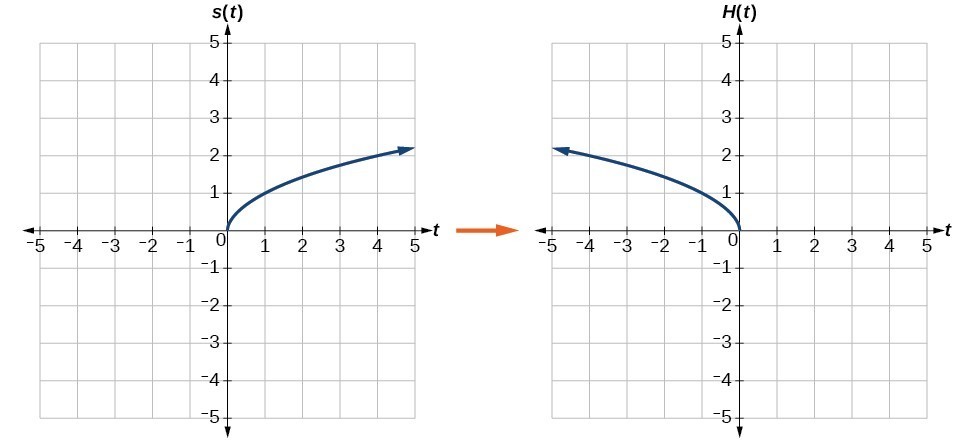
Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra

How To Reflect Quadratic Equations Video Lesson Transcript Study Com

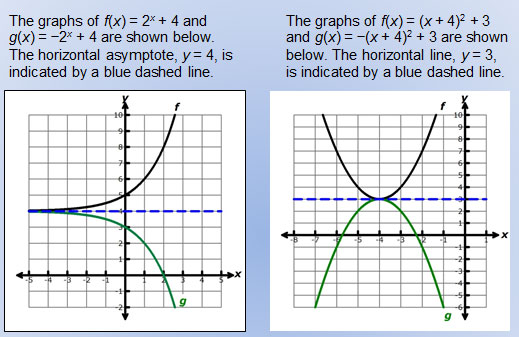
Untitled Document

Transformations Of Functions Mathbitsnotebook A1 Ccss Math

How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics

Transformation Reflection Over X Axis

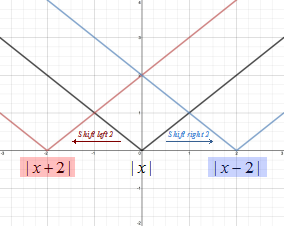
Function Transformations

Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation

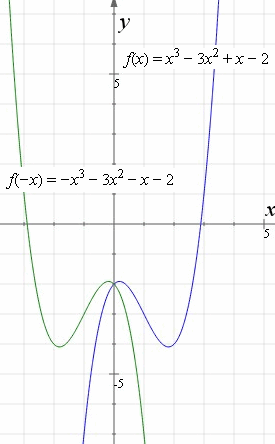
How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics

The Transformation Of The Graph Of A Quadratic Equation Matherudition

2

Horizontal

Transformations Boundless Algebra

Inverse Function Reflection In Y Axis Mathematics Stack Exchange

Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation

Reflection Over The X And Y Axis The Complete Guide Mashup Math

Transformations Reflecting Over The X Axis

Reflection Of A Point In Origin Reflected In The Origin Worked Out Examples

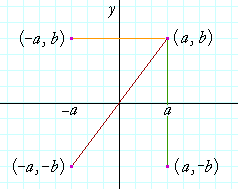
Reflections Of A Graph Topics In Precalculus

Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines

How To Reflect Quadratic Equations Video Lesson Transcript Study Com

Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line

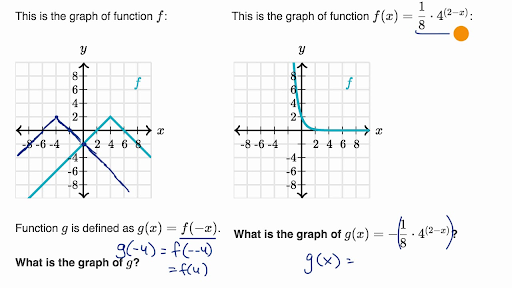
Reflecting Functions Examples Video Khan Academy

Using Transformations To Graph Functions

Solution What Is The Equation Of The Curve Y X 3 After It Is Reflected In The X Axis

Coordinate Plane

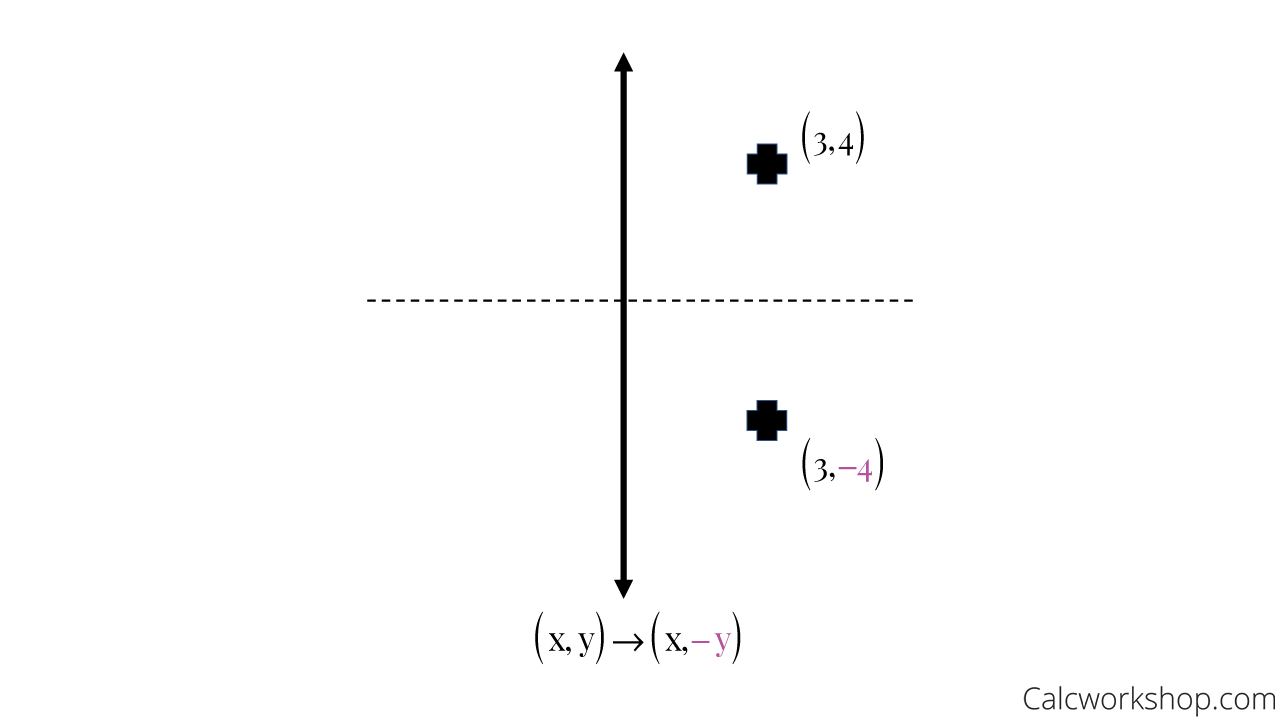
Reflection Rules How To W 25 Step By Step Examples

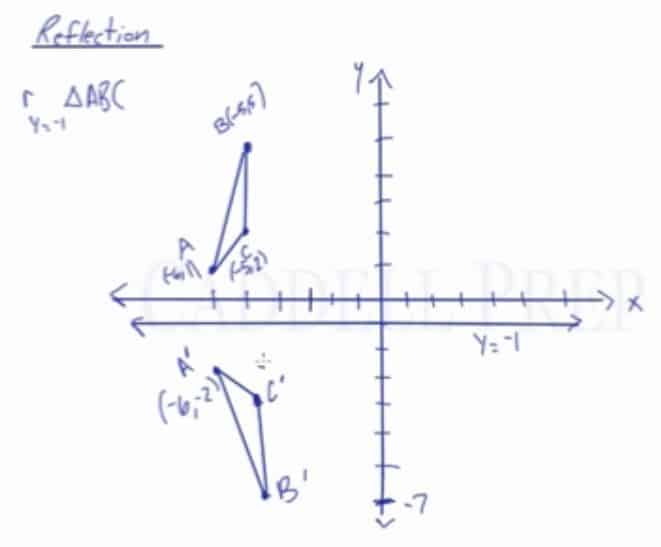
Learn About Reflection Over A Horizontal Or Vertical Line

Reflecting Functions Examples Video Khan Academy

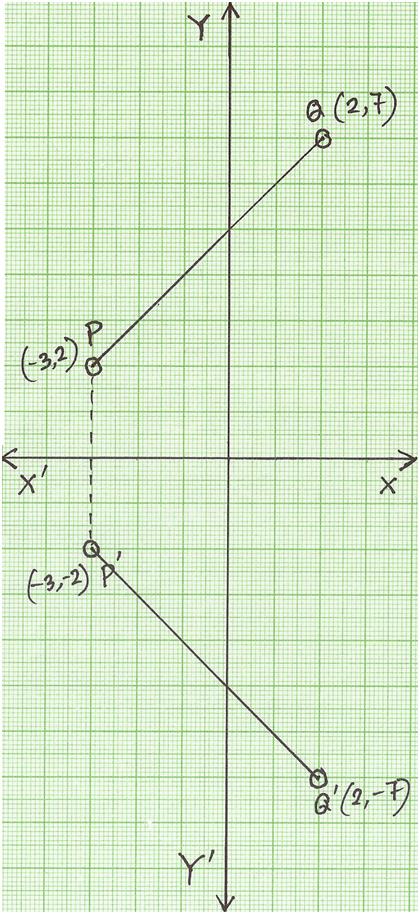
Reflection Of A Point In X Axis Reflection Of A Point Reflection

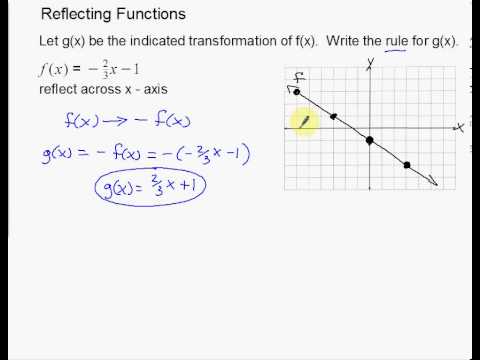
Linear Reflections Across X And Y Axis Example Youtube

1

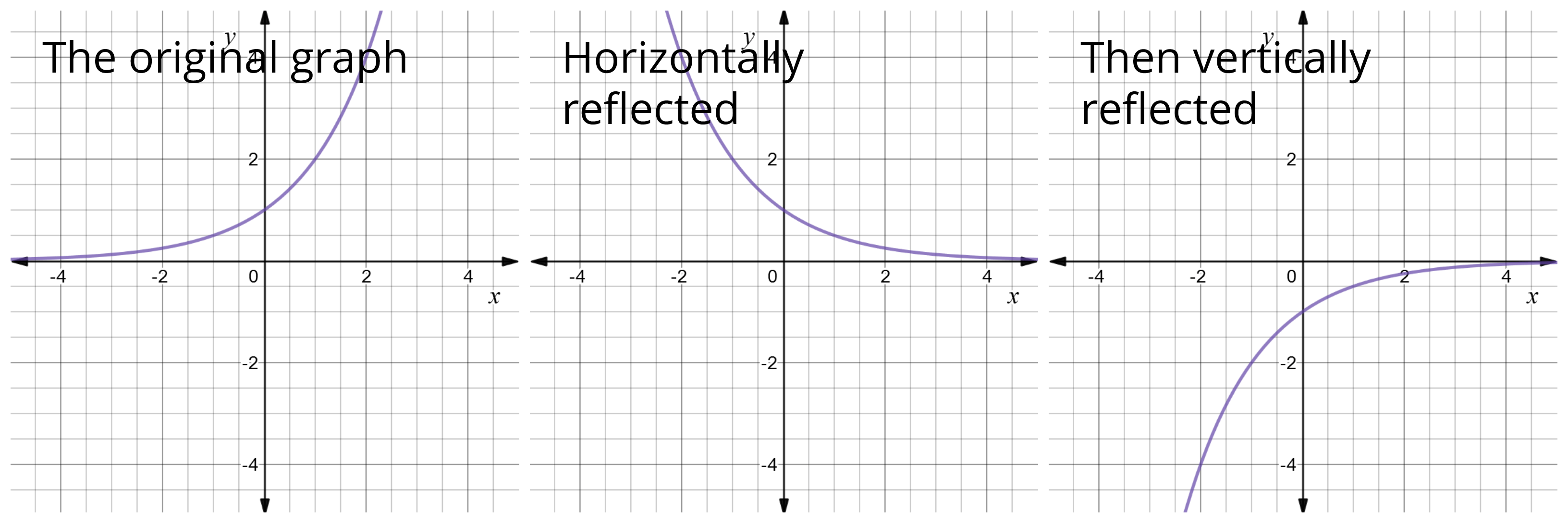
Reflect Function About Y Axis F X Expii

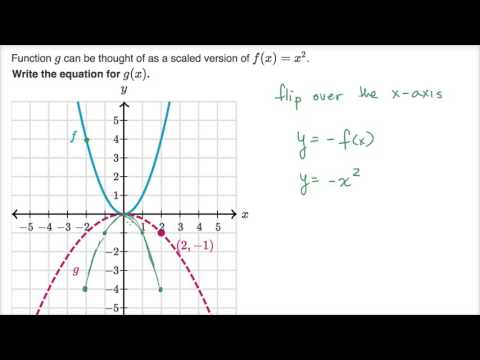
Scaling Reflecting Parabolas Video Khan Academy

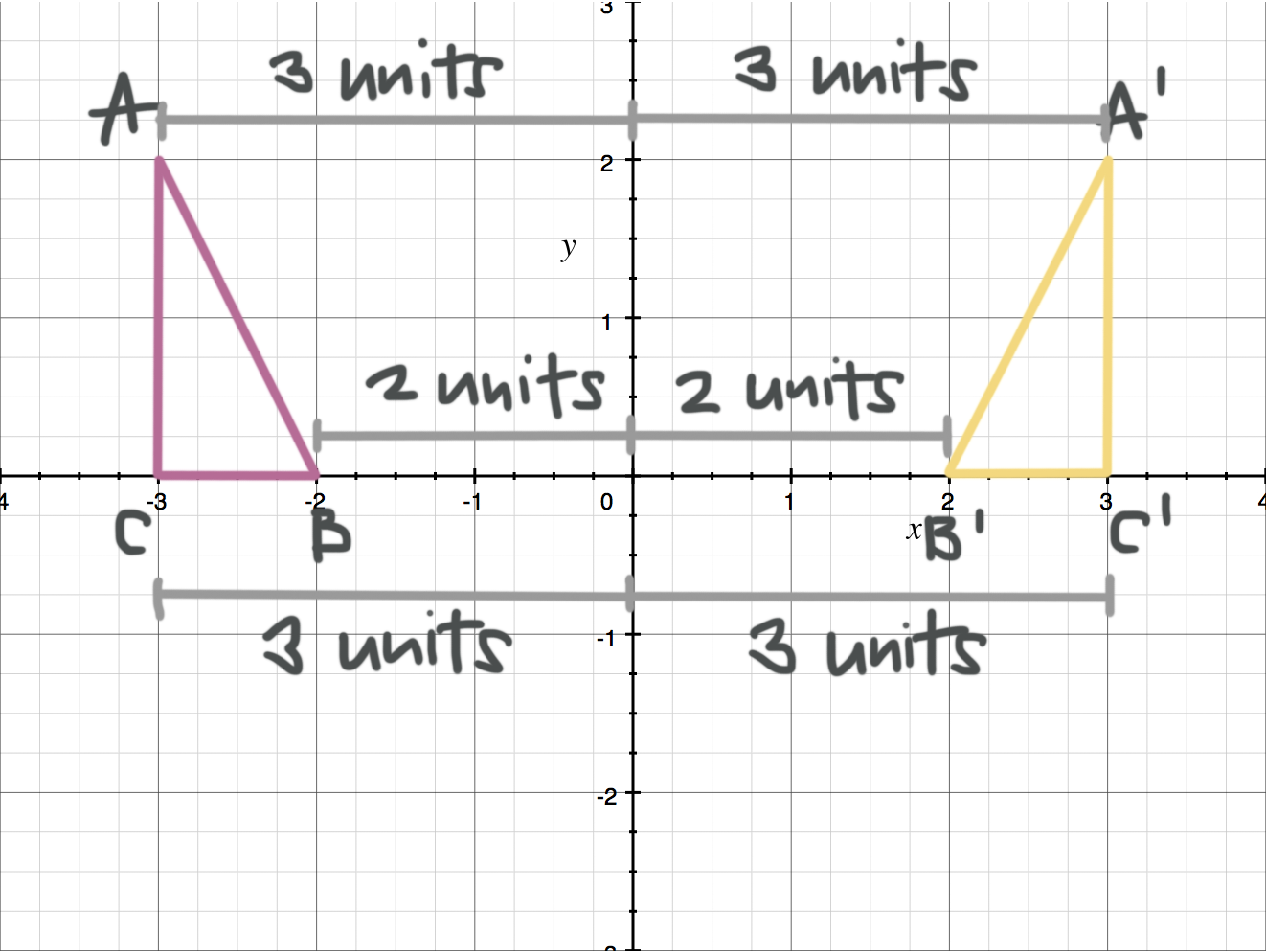
Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor

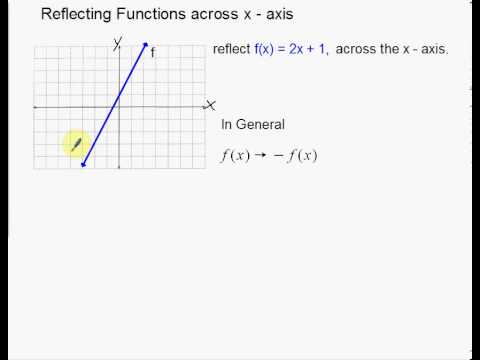
Linear Reflections Across X And Y Axis Youtube

Reflection

Reflection Transformation Matrix

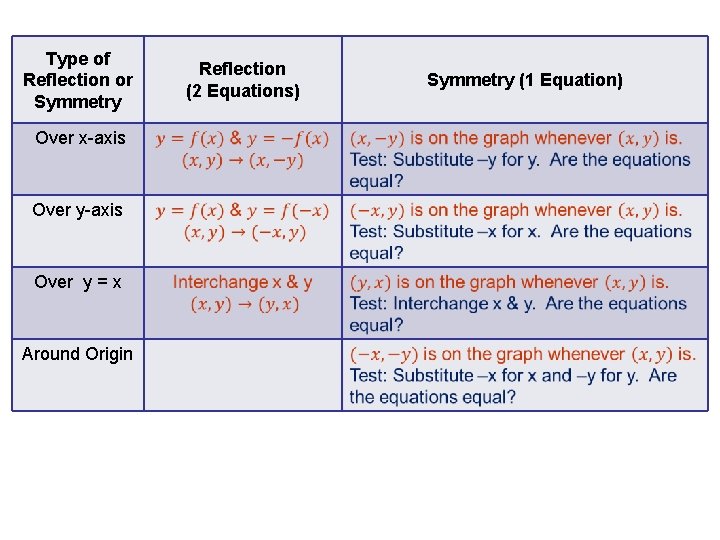
Warm Up Use The Graph To Give The

Scaling Reflecting Parabolas Video Khan Academy

Common Reflections Key Stage 3

1 5 Shifting Reflecting And Stretching Graphs

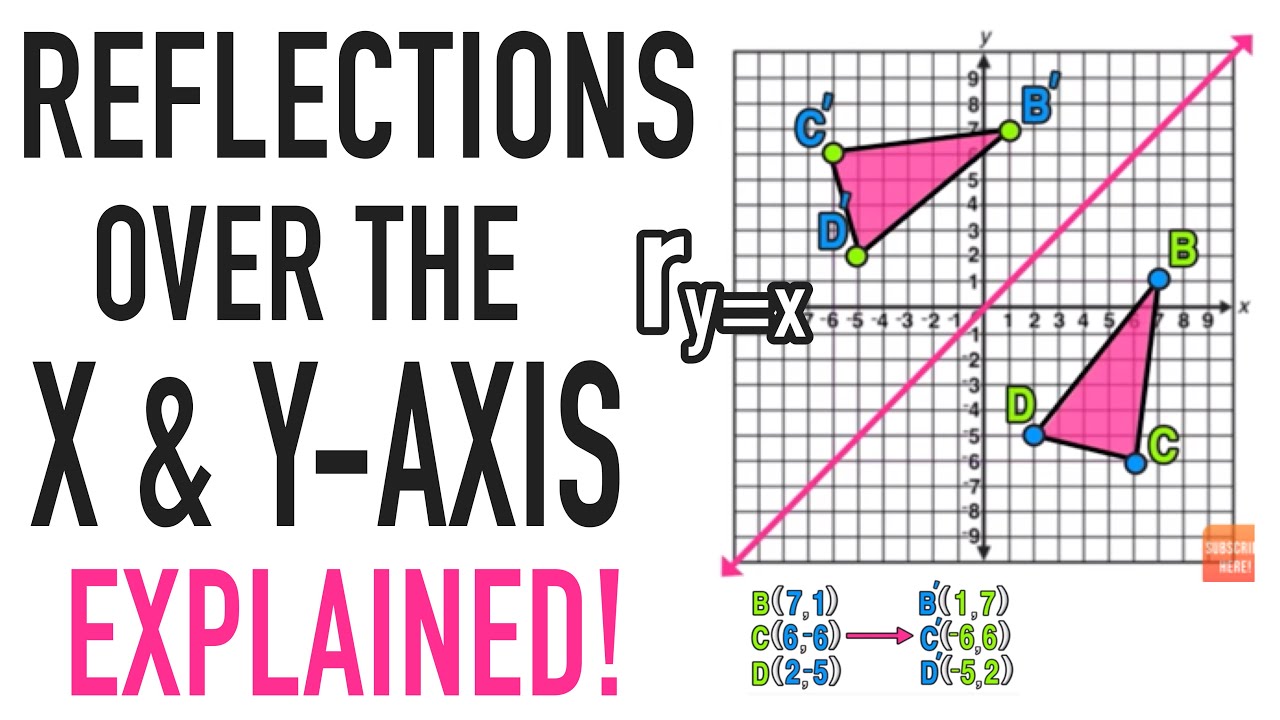
Reflections Over The X Axis And Y Axis Explained Youtube

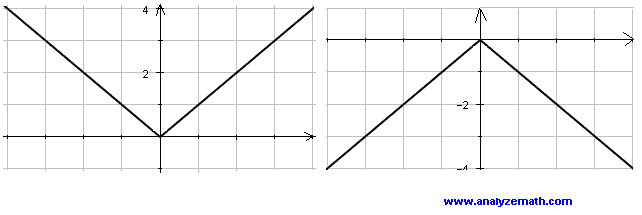
Graphing By Translation Scaling And Reflection

Reflection Over The X And Y Axis The Complete Guide Mashup Math

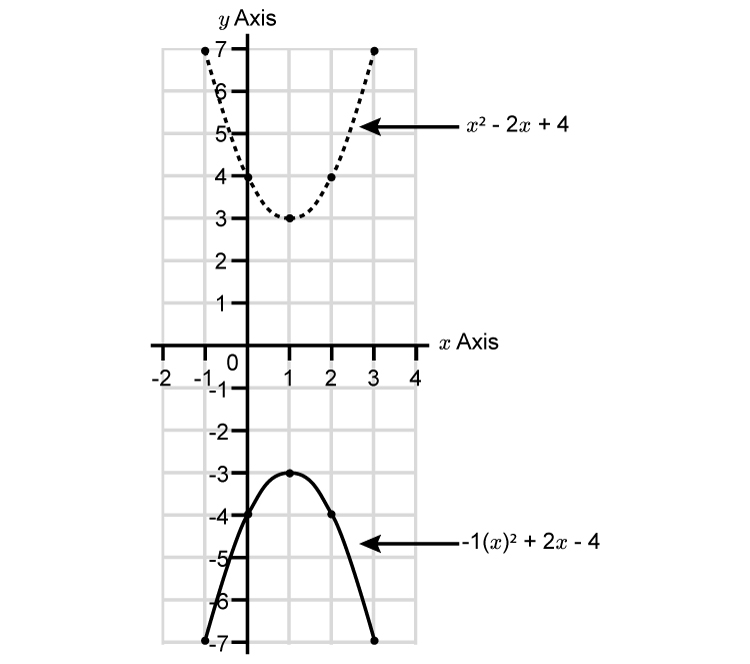
Reflecting More Difficult Parabolas Mammoth Memory Maths

Reflections

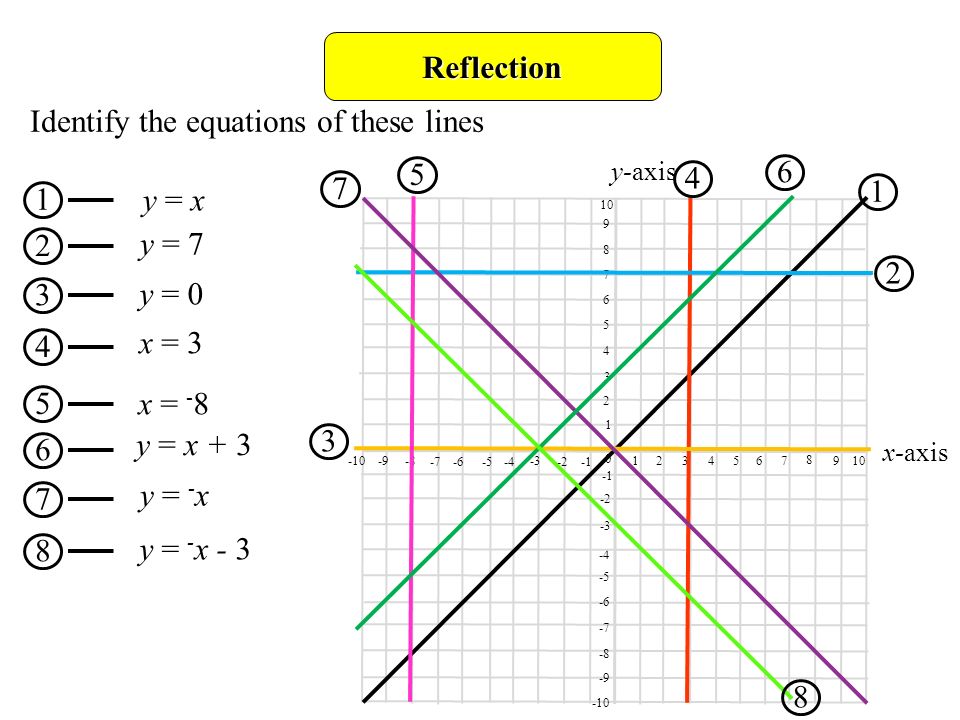
Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download

Lesson Worksheet Function Transformations Reflection Nagwa

Incoming Term: reflection over x or y axis in equation,